🧭 3D-Compass: Navigating the Spherical World

STEM Workshop for Middle/High School Math \& Science

Visualization Tool: The Spherical Coordinate System

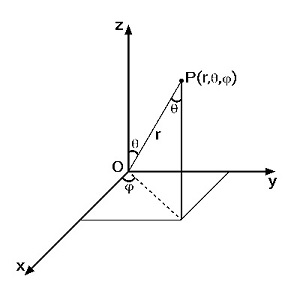
Spherical Coordinate System Diagram Placeholder

The 3D-Compass physically models the $\rho, \theta, \phi$ coordinates shown above.

1. Workshop Structure (90 Minutes)

This session uses the **Engineering Design Process (EDP)**, ensuring students transition from abstract formulas to tangible, measurable solutions.

Phase 1: Explore & Define (15 Min)

Introduce 3D location challenge. Define the **Project Phoenix Challenge**: convert a spherical target location ($\rho, \theta, \phi$) into rectangular coordinates ($x, y, z$) for vehicle navigation.

Phase 2: Learn & Practice (35 Min)

Hands-on use of the 3D-Compass to set angles ($\theta, \phi$). Guided practice applying trigonometric conversion rules.

Phase 3: Design & Test (30 Min)

Teams calculate $x, y, z$ for a unique target, then physically set the coordinates on the 3D-Compass and verify the vector's direction against a scaled grid model.

Phase 4: Share & Reflect (10 Min)

Teams analyze measurement error, discuss how the coordinate system conventions change between math (Zenith) and real-world (Declination), and connect the skills to STEM careers.

**Core Problem:** **Project Phoenix: Target Acquisition Challenge** - Convert $\rho=15.0 \text{ km}$, $\theta=35^\circ$ (Elevation), $\phi=120^\circ$ (Azimuth) to $x, y, z$ coordinates.

2. LSSS Standards Alignment Matrix (EBR/Louisiana)

The workshop directly supports the Louisiana Student Standards (LSSS) across three core disciplines, reinforcing Science and Engineering Practices (SEP).

Mathematics

(LSSS: F-TF.A.2 / N-VM.A.1)

**Focus:** Trigonometric functions, vector analysis, and 3D geometry applications (Algebra II / Pre-Calculus).

Science

(LSSS: HS-ESS1-4)

**Focus:** Modeling orbital motions, frame of reference, and coordinate system dynamics (Earth Science / Physics).

Engineering

(LSSS: HS-ETS1-2)

**Focus:** Utilizing the Engineering Design Process (EDP) to design, test, and optimize measurement solutions.

Technology

(LSSS: K-12.CS.A.2)

**Focus:** Computational thinking, abstraction, and data representation through pseudocode and modeling (Computer Science).

3. Assessment Rubric (Measurable Criteria)

Performance is assessed based on the following four measurable criteria:

Criterion	Description
1. Mathematical Accuracy	Assesses correct application of trigonometric formulas and notation (LSSS: F-TF.A.2).
2. Model Application & Precision	Measures the accuracy ($\pm 1^\circ$ tolerance) and correct physical use of the 3D-Compass instrument (SEP: Developing Models).
3. Engineering Design	Evaluates the stability and functional optimization of prototyped solutions (e.g., field mount design) (LSSS: HS-ETS1-2).
4. Conceptual Understanding	Assesses the ability to explain complex concepts, such as the difference between fixed (Equatorial) and dynamic (Horizontal) coordinate systems.

4. Challenge Extensions (Activities A - F)

These optional activities provide opportunities for differentiated instruction, deepening the application of Math and Science principles.

A: Engineering Design: Field Mount

Design a stable, adjustable tripod or mount for the 3D-Compass using simple materials (paper, straws). The design must minimize angular wobble ($\pm 0.5^{\circ}$) under field conditions.

B: Computational Conversion Code

Write pseudocode or Python/JavaScript functions that automate the conversion between $\rho, \theta, \phi$ and $x, y, z$. Students must also account for unit conversions (degrees to radians).

C: Error Analysis & Precision Testing

Test the instrument's accuracy by taking 10 measurements of a single fixed point. Calculate the mean, standard deviation, and percentage of error in the $x, y, z$ coordinates to assess precision (LSSS: S-ID.A.4).

D: 3D Pathfinding & Vector Sums

Plan a 3D drone path requiring three sequential spherical vectors ($\rho_1, \theta_1, \phi_1$, etc.). Calculate the single resultant rectilinear vector ($\mathbf{R}$) that represents the final destination (LSSS: N-VM.A.1).

E: Global Navigation & Great Circle Distance

Use spherical geometry principles to calculate the shortest distance between two points on the Earth's surface (e.g., Baton Rouge to London) using the Haversine formula, linking the concepts to geography.

$$ d = R \cdot \arccos\left(\sin(\phi_1)\sin(\phi_2) + \cos(\phi_1)\cos(\phi_2)\cos(\lambda_2-\lambda_1)\right) $$

F: Celestial Targeting: Finding a Star

Apply the concept to astronomy by locating a fixed star (like Betelgeuse) using its Equatorial Coordinates (RA/Dec). This requires compensating for Earth's rotation to find the correct Azimuth/Polar angle at a specific time (LSSS: HS-ESS1-4).

**Example:** To locate Betelgeuse (Dec: $7^\circ 24'$ N) at midnight tonight in Baton Rouge, LA, students must determine the required Azimuth angle by calculating the star's Hour Angle (HA) relative to the local meridian.